我的推荐算法之路(2):矩阵分解

发表于 更新于 分类于 阅读次数： 本文字数： 6.9k 阅读时长 ≈ 6 分钟

前言

针对协同过滤算法的头部效应较明显、泛化能力较弱的问题，矩阵分解算法被提出。矩阵分解在协同过滤算法中“共现矩阵”的基础上，加入了隐向量的概念，加强了模型处理稀疏矩阵的能力，针对性地解决了协同过滤存在的主要问题。

一、矩阵分解

矩阵分解有几个明显的特点，它具有协同过滤的 “集体智慧”，隐语义的 “深层关系”，以及机器学习的 “以目标为导向的有监督学习”。在了解了基于邻域的协同过滤算法后，集体智慧自不必多说，我们依次从 “隐因子” 和 “有监督学习” 的角度来了解矩阵分解的基本思路。

推荐算法中的矩阵分解最初的想法是从奇异值分解（Singular Value Decomposition，SVD）借鉴来的。以 \(Netflix\) 用户对电影的评分矩阵为例，矩阵分解，直观上来说就是把原来的大矩阵，近似分解成两个小矩阵的乘积，在实际推荐计算时不再使用大矩阵，而是使用分解得到的两个小矩阵。按照矩阵分解的原理，我们会发现原来 \(m×n\) 的大矩阵会分解成 \(m×k\) 和 \(k×n\) 的两个小矩阵，这里多出来一个 \(k\) 维向量，就是隐因子向量（Latent Factor Vector）。\(k\) 的大小决定了隐向量表达能力的强弱。 \(k\) 的取值越小，隐向量包含的信息越少，模型的泛化程度越高；反之，\(k\) 的取值越大，隐向量的表达能力越强，但泛化程度相应降低。此外，\(k\) 的取值还与矩阵分解的求解复杂度直接相关。

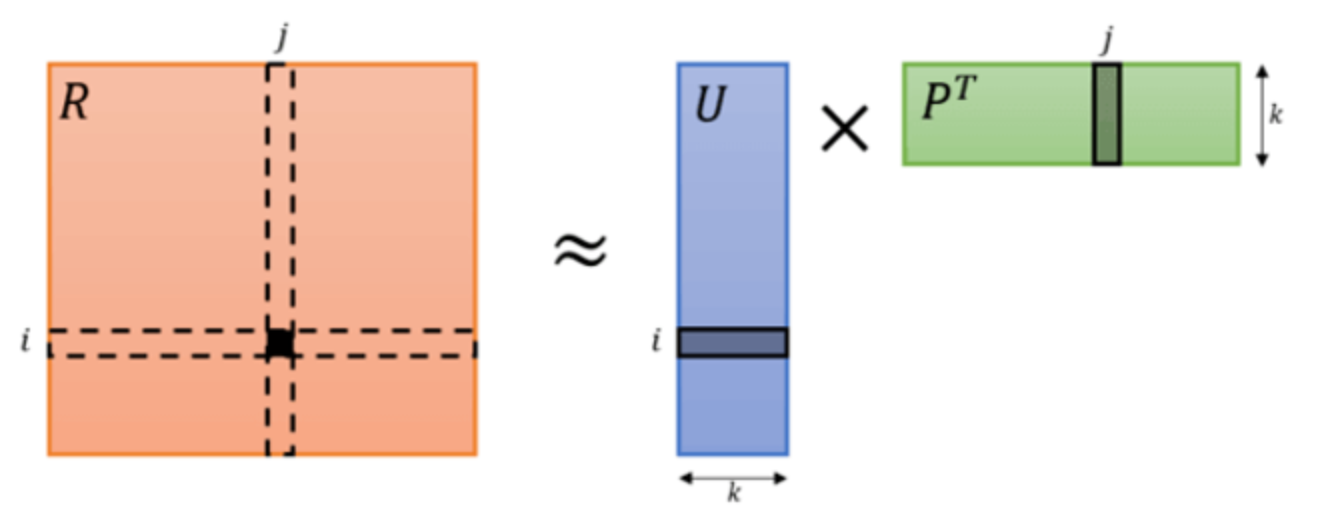
基于矩阵分解的推荐算法的核心假设是用隐向量来表达用户和物品，他们的乘积关系就成为了原始的元素。这种假设之所以成立，是因为我们认为实际的交互数据是由一系列的隐向量的影响下产生的，这些隐向量代表了用户和物品一部分共有的特征，在物品身上表现为属性特征，在用户身上表现为偏好特征，只不过这些因子并不具有实际意义，也不一定具有非常好的可解释性，每一个维度也没有确定的标签名字，所以才会叫做 “隐变量”。而矩阵分解后得到的两个包含隐变量的小矩阵，一个代表用户的隐含特征，一个代表物品的隐含特征，矩阵的元素值代表着相应用户或物品对各项隐因子的符合程度，有正面的也有负面的。

我们再从机器学习的角度来了解矩阵分解，我们已经知道评分预测实际上是一个矩阵补全的过程，在矩阵分解的时候原来的大矩阵必然是稀疏的，即有一部分有评分，有一部分是没有评分的，不然也就没必要预测和推荐了，所以整个预测模型的最终目的是得到两个小矩阵，通过这两个小矩阵的乘积来补全大矩阵中没有评分的位置。所以对于机器学习模型来说，问题转化成了如何获得两个最优的小矩阵。因为大矩阵有一部分是有评分的，那么只要保证大矩阵有评分的位置（实际值）与两个小矩阵相乘得到的相应位置的评分（预测值）之间的误差最小即可，其实就是一个均方误差损失，这便是模型的目标函数。

二、矩阵分解的优缺点

矩阵分解具有以下优点：

  • 泛化能力强。在一定程度上解决了数据稀疏的问题。
  • 空间复杂度低。不需再存储协同过滤模型所需的“庞大“用户相似性或物品相似性矩阵，只需存储用户和物品隐向量空间复杂度由 \(n^2\) 级别降低到 \((n+m)*k\) 级别。
  • 更好的扩展性和灵活性。矩阵分解最终产出的是用户和物品隐向量，这其实与深度学习中的Embedding思想不谋而合，因此矩阵分解的结果也非常便于与其他特征进行组合和拼接，与深度学习网络进行无缝组合。

矩阵分解也有一些局限性：

  • 矩阵分解不方便加入用户、物品、上下文相关的特征，丧失了利用很多有效信息的机会。
  • 在缺乏用户历史行为时，无法进行有效的推荐。
  • 模型训练比较费时。
  • 推荐结果不具有很好的可解释性，分解出来的用户和物品矩阵的每个维度无法用现实生活中的概念来解释，只能理解为潜在语义空间。

三、矩阵分解相关算法

3.1 奇异值分解SVD

有关SVD的原理阐述请参考我的相关博客：机器学习日记(四):奇异值分解

虽然奇异值分解解决了矩阵分解问题，但其存在两点缺陷，使其不宜作为互联网场景下矩阵分解的主要方法：

  • SVD 要求矩阵是稠密的，而现实场景中的共现矩阵是稀疏的，有大量空白，无法直接使用 SVD 分解。要想使用 SVD，必须对评分矩阵中的缺失值进行简单的补全，比如用全局平均值或者用用户物品平均值补全，得到补全后的矩阵。接着可以用 SVD 分解并降维。但填充本身会造成很多问题，其一，填充大大增加了数据量，增加了算法复杂度。其二，简单粗暴的数据填充很容易造成数据失真。
  • 传统奇异值分解的计算复杂度达到了 \(O(mn^2)\) 的级别，这对于商品数量动辄上百万、用户数量往往上千万的互联网场景来说几乎是不可接受的。

3.2 Funk-SVD

\(Simon　Funk\) 在博客上公开发表了一个只考虑已有评分记录的矩阵分解方法，称为 \(Funk-SVD\)，也就是被 \(Yehuda Koren\) 称为隐语义模型的矩阵分解方法。它的出发点为，既然将一个矩阵做 SVD 分解成 3 个矩阵很耗时，同时还面临稀疏的问题，那么我们能不能避开稀疏问题，同时只分解成两个矩阵呢？也就是说，现在期望我们的矩阵\(M\) 这样进行分解：

\[M_{m×n}=P_{m×k}^TQ_{k×n}\]

这种简化的矩阵分解不再是分解为三个矩阵，而是分解为两个低秩的用户和物品矩阵，其实就是把用户和物品都映射到一个 \(k\) 维空间中，这个 \(k\) 维空间对应着 \(k\) 个隐因子，我们认为用户对物品的评分主要是由这些隐因子影响的，所以这些隐因子代表了用户和物品一部分共有的特征，在物品身上表现为属性特征，在用户身上表现为偏好特征。只不过这些隐因子并不具有实际意义，也不一定具有非常好的可解释性，每一个维度也没有确定的标签名字，所以才会叫做 “隐因子”。

我们知道 \(SVD\) 分解已经很成熟了，但是 \(Funk-SVD\) 如何将矩阵 \(M\) 分解成为 \(P\) 和 \(Q\) 呢？这里采用了线性回归的思想。我们的目标是让用户的评分和用矩阵乘积得到的评分残差尽可能的小，也就是说，可以用均方差作为损失函数，来寻找最终的P和Q。即通过 User-Item 评分信息来学习到的用户特征矩阵 \(P\) 和物品特征矩阵 \(Q\)，通过重构的低维矩阵预测用户对物品的评分。

对于某一个用户评分 \(m_{ij}\) 如果用 \(Funk-SVD\) 进行矩阵分解，则对应的表示为 \(q_j^Tp_i\)，采用均方差作为损失函数，则我们期望 \((m_{ij}-q_j^Tp_i)^2\) 尽可能的小，如果考虑所有的物品和样本的组合，则我们期望最小化下式：

\[\sum_{i,j}(m_{ij}-q_j^Tp_i)^2\]

只要我们能够最小化上面的式子，并求出极值所对应的 \(p_i,q_j\)，则我们最终可以得到矩阵 \(P\) 和 \(Q\)，那么对于任意矩阵 \(M\) 任意一个空白评分的位置，我们可以通过 \(q_j^Tp_i\) 计算预测评分，很漂亮的方法！

当然，在实际应用中，为了防止过拟合，会加入一个 \(L2\) 的正则化项，因此正式的 \(Funk-SVD\) 的优化目标函数是这样的：

\[arg\mathop{min}\limits_{p_i,q_j}\sum_{(i,j)\in K}(m_{ij}-q_j^Tp_i)^2+\lambda(||p_i||^2_2+||q_j||^2_2)\]

其中 \(K\) 为已有评分记录的 \((i,j)\) 对集合，\(m_{ij}\) 为用户 \(i\) 对物品 \(j\) 的真实评分，\(\lambda\) 是正则化系数。对于这个优化问题，一般通过梯度下降法来进行优化得到结果。

将上式分别对 \(p_i,q_j\) 求导：

\[\frac{∂J}{∂p_i} = -2(m_{ij}-q_j^Tp_i)q_j+2\lambda p_i\]

\[\frac{∂J}{∂q_j} = -2(m_{ij}-q_j^Tp_i)p_i+2\lambda q_j\]

则在梯度下降法迭代时，\(p_i,q_j\) 的迭代公式为：

\[p_i = p_i + \alpha ((m_{ij}-q_j^Tp_i)q_j-\lambda p_i)\]

\[q_j = q_j + \alpha ((m_{ij}-q_j^Tp_i)p_i-\lambda q_j)\]

3.3 Bias-SVD

在 \(Funk-SVD\) 算法火爆之后，出现了很多 \(Funk-SVD\) 的改进版算法。其中 \(Bias\) 算是改进的比较成功的一种算法。其在 \(Funk-SVD\) 的基础上加了偏置项特征。

由于不同用户的打分体系不同（比如在5分为满分的情况下，有的用户认为打3分已经是很低的分数了，而有的用户认为打1分才是比较差的评价），不同用户的衡量标准也有所区别（比如电子产品的平均分和日用品的平均分差异有可能比较大），为了消除用户和物品打分的偏差（Bias），常用的做法是在矩阵分解时加入用户和物品的偏差向量，如下所示：

\[r_{ui} = \mu + b_i + b_u + q_j^Tp_i\]

偏置部分主要由三个子部分组成：

  • 训练集中所有评分记录的全局平均数 \(\mu\) ，表示了训练数据的总体评分情况，对于固定的数据集，它是一个常数。
  • 用户偏置 \(b_u\)，独立于物品特征的因素，表示某一特定用户的打分习惯。例如，对于批判性用户对于自己的评分比较苛刻，倾向于打低分；而乐观型用户则打分比较保守，总体打分要偏高。
  • 物品偏置 \(b_i\) ，特立于用户兴趣的因素，表示某一特定物品得到的打分情况。以电影为例，好片获得的总体评分偏高，而烂片获得的评分普遍偏低，物品偏置捕获的就是这样的特征。

加入了偏置项以后的优化目标函数如下所示：

\[arg\mathop{min}\limits_{p_i,q_j}\sum_{(i,j)\in K}(m_{ij}-q_j^Tp_i-\mu-b_i-b_u)^2+\lambda(||p_i||^2_2+||q_j||^2_2+||b_i||^2_2+||b_u||^2_2)\]

四、基于Pytorch的矩阵分解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
# Bias-SVD代码实现
# 基于MovieLens 1M数据集

from moviesData import readRatings
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
from sklearn.model_selection import train_test_split

class MFDataset(Dataset):
    def __init__(self, u_id, i_id, rating):
        self.u_id = u_id
        self.i_id = i_id
        self.rating = rating

    def __getitem__(self, index):
        return self.u_id[index], self.i_id[index], self.rating[index]

    def __len__(self):
        return len(self.rating)

class MF(nn.Module):
    def __init__(self, num_users, num_items, mean, embedding_size=100):
        super().__init__()
        self.user_emb = nn.Embedding(num_users, embedding_size) # 隐向量
        self.user_bias = nn.Embedding(num_users, 1)  # 用户偏置
        self.item_emb = nn.Embedding(num_items, embedding_size) # 隐向量
        self.item_bias = nn.Embedding(num_items, 1)  # 物品偏置
		
        # 参数初始化
        self.user_emb.weight.data.uniform_(0, 0.005)  # 0-0.05之间均匀分布
        self.user_bias.weight.data.uniform_(-0.01, 0.01)
        self.item_emb.weight.data.uniform_(0, 0.005)
        self.item_bias.weight.data.uniform_(-0.01, 0.01)
		
        # 全局偏置
        # 将不可训练的tensor转换成可训练的类型parameter，并绑定到module里，net.parameter()中就有了这个参数
        self.mean = nn.Parameter(torch.FloatTensor([mean]), False)

    def forward(self, u_id, i_id):
        U = self.user_emb(u_id)
        b_u = self.user_bias(u_id).squeeze()
        I = self.item_emb(i_id)
        b_i = self.item_bias(i_id).squeeze()
        return (U * I).sum(1) + b_u + b_i + self.mean # 返回预测评分

def train(model, x_train, y_train, loss_func):
    train_ls = [] # 返回训练误差
    train_dataset = MFDataset(x_train[:, 0], x_train[:, 1], y_train)
    # DataLoader将一个batch_size封装成一个tensor，方便迭代
    train_iter = DataLoader(train_dataset, batch_size=1024)
	
    # weight_decay是正则化系数
    optimizer = torch.optim.Adam(model.parameters(), lr=1e-4, weight_decay=0.1)
    model = model.float()
    for epoch in range(50):
        model.train()  # 如果模型中有Batch Normalization或Dropout层，需要在训练时添加model.train()，使起作用
        total_loss, total_len = 0.0, 0
        for x_u, x_i, y in train_iter:
            y_pred = model(x_u, x_i)
            l = loss_func(y_pred, y).sum()
            optimizer.zero_grad() # 清空这一批的梯度
            l.backward() # 回传
            optimizer.step() # 参数更新

            total_loss += l.item()
            total_len += len(y)
        train_ls.append(total_loss / total_len)
    return train_ls

if __name__ == '__main__':
    pd.set_option('display.max_rows', 1000, 'display.max_columns', None,
                  'display.float_format', lambda x:"%.2f" % x)
    path = r'C:\Users\QzmVc1\Desktop\MovieLens'
    df = readRatings(path)

    x, y = df.iloc[:, :2], df.iloc[:, 2]
    x = torch.tensor(x.values, dtype=torch.int64)
    y = torch.tensor(y.values, dtype=torch.float32)

    x_train, x_test, y_train, y_test = train_test_split(x.numpy(), y.numpy(), test_size=0.3, random_state=1)

    mean_rating = df.iloc[:, 2].mean()
    # 虽然数据集的UserID是从1开始的，但这里还是需要+1，因为nn.Embedding是从索引0开始，而model(x_u, x_i)传的是真实的ID
    num_users, num_items = df['UserID'].max()+1, df['MovieID'].max()+1

    model = MF(num_users, num_items, mean_rating)
    loss = nn.MSELoss(reduction='sum')

    train_ls = train(model, x_train, y_train, loss)
    print(train_ls)