我的推荐算法之路(10):Cross-domain Recommendation via Deep Domain Adaptation
一、前言
传统的推荐系统通常对用户过去的交互(例如评分或点击)做出假设来做出有意义的推荐。虽然这看起来很自然,但是,当假设不成立时,例如当新用户到达或我们的目标是对未使用的产品进行交叉销售时,这种系统的实用性就会降低。另一方面,随着网络服务种类的增加,冷启动用户的信息可以从他们在其他服务中的活动中获得。因此,利用来自其他相关领域的此类附加信息的跨域推荐系统近年来作为解决用户冷启动问题的有希望的解决方案获得了研究的关注 。
针对处理冷启动用户的跨域推荐,特别是在没有共同用户和item的情况。尽管可以推荐item并从目标用户那里获得反馈,但我们的目标是构建一个推荐系统,即使在这种替代方案不可用的情况下也可以工作。在这种情况下,一个主要的挑战是由于缺乏共同的用户,传统的方法不能用于两个服务之间的关系的引出。
该文研究了基于内容的方法,特别是,研究了一种跨域推荐的深度学习方法。深度学习已成功应用于推荐系统,除了在推荐系统应用中的成功之外,深度学习方法在迁移学习领域表现出更好的性能,因为它能够从数据中学习可迁移的特征。事实上,在领域自适应领域,深度神经网络在计算机视觉和自然语言处理任务中表现出最先进的性能。基于这一观察,该文假设深度神经网络的域适应也可以应用于跨域推荐。
领域自适应(Domain Adaptation)是一种使用从具有标记数据的一个域(源域)获得的知识来学习具有少量或没有标记训练数据的新域(目标域)的技术。通过域适应,可以将在源域中训练的分类器应用于目标域。为了实现领域自适应,该文使用了一种用于无监督域适应的神经网络架构,即 Bousmalis 等人提出的域分离网络(DSN)。此外,为了降低极端分类的难度和处理新item,该文通过堆叠去噪自动编码器(SDAE)来结合item特征。
原文链接:Cross-domain Recommendation via Deep Domain Adaptation
二、模型架构
在该文中,假设输入数据采用隐式反馈的形式,例如点击日志。令 \(Y=\{1,2,\cdots,L\}\) 是我们希望推荐的源域中的item集合。从用户对这些items的日志信息中,我们可以得到一个有标记的数据集 \(X_S=\{x_i^S,y_i^S\}_{i=1}^{N_s}\)。这里 \(y_i^S\) 表示一个标签,\(x_i^S\) 表示item的原始特征。在目标域中,由于两个域之间缺乏共同用户,我们只有一个未标记的数据集 \(\{x_i^T\}_{i=1}^{N_T}\)。我们的目标是向目标域中的用户推荐源域中的item。更正式地说,通过利用标记数据 \(X_S\) 和未标记数据 \(X_T\),我们的目标是构建一个分类器 \(\eta(x^T)\),它定义了给定目标域中用户历史 \(X^T\) 关于源域item集合 \(Y\) 的概率分布。我们使用域分离网络 \(DSN\) 对这个分类器进行建模。
例如,假设我们的任务是向使用新闻浏览服务的用户推荐视频。我们有源域中的视频服务和目标域中的新闻服务的用户日志。视频可以包含有关其自身的文本信息,例如演员或情节的描述。有了这些内容信息,我们可以使用 Bag of Words 或 TF-IDF 方案从视频列表中构建原始用户表示。与视频一样,我们可以使用新闻文章的文本信息为新闻用户构建表示。使用内容信息,我们获得源域(视频服务)的标记数据集和目标域(新闻服务)的未标记数据集。在这种情况下,任务是建立一个分类器,将新闻浏览历史作为输入,并为视频分配概率。
同时,我们也使用到了堆叠去噪自动编码器 (SDAE)。 它是一个前馈神经网络,可以学习输入数据的稳健表示。
该文模型架构如下图所示,接下来,将对DSN和SDAE做一个详细介绍。
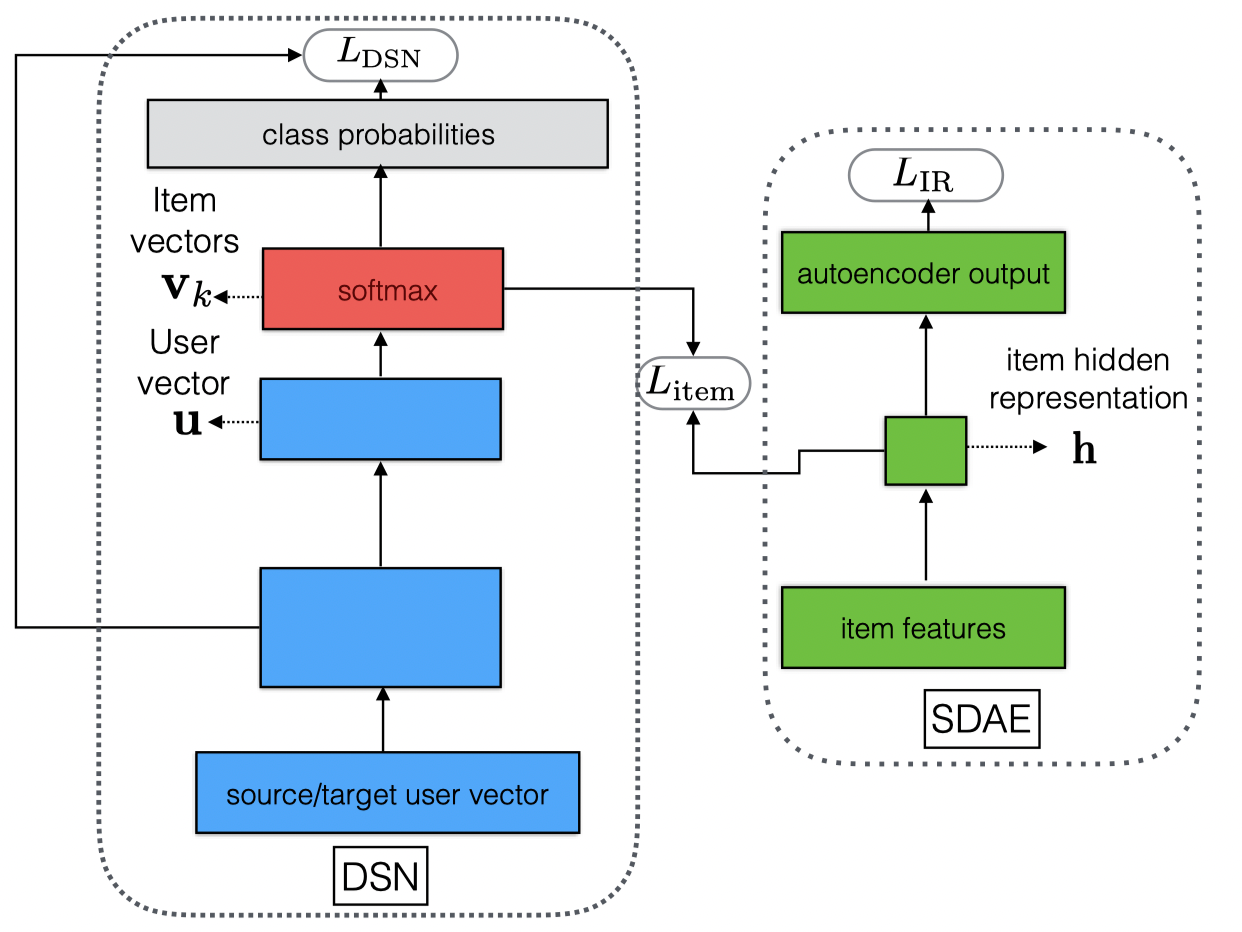
三、Domain Separation Networks(DSNs)
3.1 简介
DSNs模型的作者是来自谷歌的研究者,该文发表在2016年的NIPS会议上,在这篇论文中,作者的工作重心放在了迁移学习三个核心问题之一:what to transfer,以及如何有效避免negative transfer上。在论文伊始,作者就提出之前已有的深度迁移学习算法都将注意力放在消除不同域之间的特征分布差异,但是Konstantinos Bousmalis(作者)等人从另一个角度来考虑了迁移学习问题,他们认为所有的域之间有着公有的特征(Shared)和私有的特征(Private),如果将各个域的私有特征也进行迁移的话就会造成负迁移(negative transfer)。基于这一理念,他们提出了Domain Separation Networks(DSNs)。同时,作者为问题假设的前提是无监督迁移学习,也就是说目标域数据是没有标记的,源域数据有标记。因此,DSNs的主要工作分为两部分:
- 提取不同域之间的公有特征
- 利用公有特征进行迁移
3.2 DSNs模型
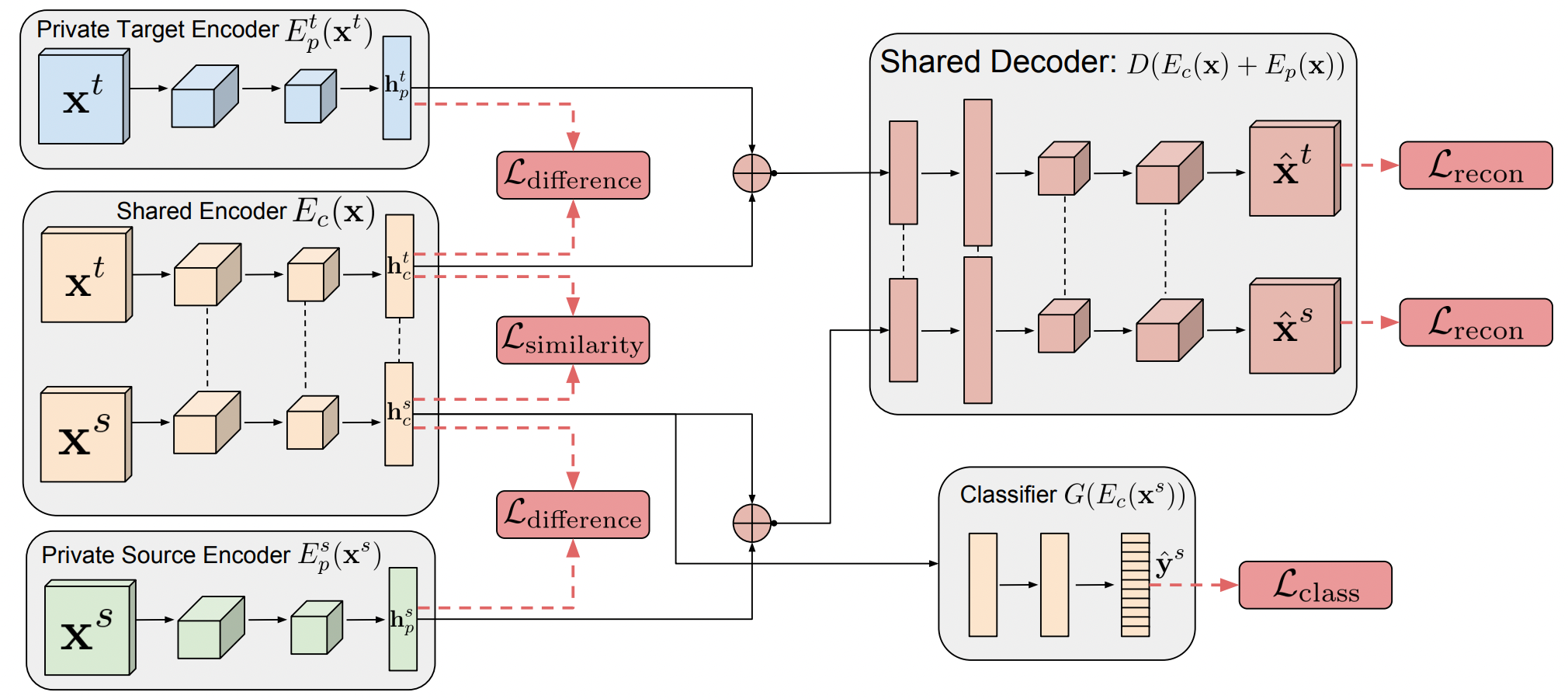
DSNs的主体结构是一个类似于自编码器的结构。整个结构可以分为如下五部分:
- Private Target Encoder \(E_p^t(x^t)\) : 目标域私有编码器,用来提取目标域的私有特征。
- Private Source Encoder \(E_p^s(x^s)\) : 源域私有编码器,用来提取源域的私有特征。
- Shared Encoder \(E_c(x)\) : 共享编码器,用来提取源域和目标域的公有特征。
- Shared Decoder \(D(E_c(x)+E_p(x))\) : 共享解码器,用来将私有特征和公有特征组成的样本进行解码。
- Classifier \(G(E_c(x^s))\) : 分类器,在训练时用来对源域样本进行分类,在训练完成时就可以直接用在目标域数据上进行分类。
看过每个部分的功能之后其实整个结构的原理就很明了了,首先我们忽略右下角的分类器,那么剩下的部分就是自编码器的结构。源域样本 \(x^s\) 首先进入 \(E_p^s(x^s)\) 和 \(E_c(x)\),之后两个编码器分别输出 \(h_p^s\) 和 \(h_c^s\)。 \(h_p^s\) 和 \(h_c^s\) 分别对应着源域数据中的私有特征和公有特征,同理, \(h_p^t\) 和 \(h_c^t\) 分别对应着目标域数据中的私有特征和公有特征。从上述的原理介绍我们可以知道,如果DSNs想要取得较好的效果,那么公有部分必须是真实的源域和目标域共有的特征,同时公有部分和私有部分必须完全分开,才能有效的避免负迁移,所以作者提出了以下两种损失函数来约束 \(E_p^t(x^t)\),\(E_p^s(x^s)\) 和 \(E_c(x)\) ,首先是差异损失 \(L_{difference}\):
\[L_{difference}=||{H_c^s}^TH_p^s||^2_F+||{H_c^t}^TH_p^t||^2_F\]
\(L_{difference}\) 其实计算的是 \(h_p^s\) 和 \(h_c^s\) 以及 \(h_p^t\) 和 \(h_c^t\) 的相似度大小,当 \(h_p^s=h_c^s\) 以及 \(h_p^t=h_c^t\) 时最大,当 \(h_p^s\) 和 \(h_c^s\) 正交(完全不同)以及 \(h_p^t\) 和 \(h_c^t\) 正交时 \(L_{difference}\) 最小。所以通过最小化 \(L_{difference}\) 可以达到 \(h_p^s\) 和 \(h_c^s\) 以及 \(h_p^t\) 和 \(h_c^t\) 完全分开的目的。
完全分开 \(h_p^s\) 和 \(h_c^s\) 以及 \(h_p^t\) 和 \(h_c^t\) 是不够的,因为我们还要保证 \(h_c^s\) 和 \(h_c^t\) 是可以进行迁移的,也就是要将两者进行适配,直观体现就是提高两者的相似度,因此作者提出了两种相似损失 \(L_{similarity}\):\[L_{similarity}^{DANN}=\mathop{\sum}\limits_{i=0}^{N_s+N_t}\{d_ilog\hat{d}_i+(1-d_i)log(1-\hat{d}_i)\}\]
\[L_{similarity}^{MMD}=\frac{1}{(N_s)^2}\mathop{\sum}\limits_{i,j=0}^{N_s}k(h_{ci}^s,h_{cj}^s)-\frac{2}{N_sN_t}\mathop{\sum}\limits_{i,j=0}^{N_s,N_t}k(h_{ci}^s,h_{cj}^t)+\frac{1}{(N_t)^2}\mathop{\sum}\limits_{i,j=0}^{N_t}k(h_{ci}^t,h_{cj}^t)\]
第一种相似损失是借用DANN算法中的损失函数,使用了对抗网络的思想,第二种损失函数则是迁移学习中经常用到的MMD损失。这两种损失都衡量了 \(h_c^s\) 和 \(h_c^t\) 差异的大小,因此当 \(L_{similarity}\) 最小时可以使 \(h_c^s\) 和 \(h_c^t\) 最相似甚至变为同一种分布。当 \(h_c^s\) 和 \(h_c^t\) 的分布近似相等时,在 \(h_c^s\) 上有效的分类器同样也可以在 \(h_c^t\) 上工作了。
到这里工作还远远没有结束,因为我们虽然保证了 \(h_p^s\) 和 \(h_c^s\) 以及 \(h_p^t\) 和 \(h_c^t\) 完全分开同时 \(h_c^s\) 和 \(h_c^t\) 的分布近似相等,但是我们没有保证源域数据和目标域数据的完整性。举一个极端的例子,假如无论什么数据进来都有 \(h_p^s=h_p^t=0,h_c^s=h_c^t=1\),那么上面的损失函数都是可以达到最小的,但是学到的东西却毫无意义。这时候作者采用的这种‘编码-解码’结构就起作用了,这种结构不仅能够保证提取公有、私有特征,还能够保证特征的完整性和有效性。具体的,作者为Shared Decoder提出了重构损失 \(L_{recon}\):
\[L_{recon}=\mathop{\sum}\limits_{i=1}^{N_s}||x_i^s-\hat{x}_i^s||^2+\mathop{\sum}\limits_{i=1}^{N_t}||x_i^t-\hat{x}_i^t||^2\]
到此,源域样本进入编码器到从解码器出来的过程中,两个解码器分别提取了私有和公有特征,同时又因为解码器要求公有特征和私有特征组合在一起要能够构成完整的源域样本,所以又保证了特征的完整性。同理,当目标域样本进入时也是同样的操作。但是,通过‘编码-解码’这种无监督方法提取出来了源域和目标域的公有特征以及各自的私有特征,我们还无法对样本进行分类,所以作者在整个结构中加入了分类器 \(G(E_c(x^s))\),其损失函数为:
\[L_{class}=-\mathop{\sum}\limits_{i=1}^{N_s}y_i^s\cdot log\hat{y}_i^s\]
这一步骤在迁移学习中就很常见了,在前面的过程中,自编码器已经提取出来了源域和目标域的公有部分,并且通过最小化 \(L_{similarity}\) 使两者在分布上进行了逼近。那么可以说如果一个分类器在源域的公有部分上有效的话那么在目标域的公有部分上同样有效,因此在训练时只需要使用带标记的源域数据对分类器进行训练,在训练完成时分类器就可以直接应用在目标域上了。至此,整个DSNs的各个部分都已经向大家介绍完成。
四、Stacked Denoising Autoencoder(SDAE)
论文中使用到了堆叠去噪自动编码器 (SDAE)。 它是一个前馈神经网络,可以学习输入数据的稳健表示。记 \(X_I=\{x_i\}_{i=1}^n\) 原始输入向量的集合,\(\tilde{X}_I=\{\tilde{x}_i\}_{i=1}^n\) 是含噪声的向量集合。SDAE以 \(\tilde{X}_I\) 作为输入,并通过它的编码器 \(E_\theta\) 将其转化为隐层中间向量 \(h\)。接着通过解码器 \(D_{\theta'}\) 将 \(h\) 重构,原始输入向量 \(X_I\) 即重构结果,损失函数即二者的均方损失。
五、Proposed Method
我们的目的是向目标域的用户推荐源域中的item,如前文所示,我们使用DSNs基于源域的有标签数据构建了一个分类器。对于DSNs的输出层,我们使用softmax层,该层第k个元素的值如下所示:
\[(G(E_c(x^s))_k=p(y=k|x^s)=\frac{exp(v_k^Tu)}{\mathop{\sum}\limits_{k'\in Y}exp(v_{k'}^Tu)}\]
\(v_k\) 是softmax层的权重向量,向量 \(u\) 是前一层经过激活后的结果。
由于items的数量通常很大,因此仅使用用户特征进行预测将是一项艰巨的任务。在实践中,输入数据是不平衡的,有些标签只能观察几次。此外,目标域中用户偏好的item类型可能与训练数据中的不同。因此,分类器应该能够预测训练数据中未观察到的新item。从这些观察中,我们相信结合item特征将有助于预测。事实上,在我们用于实验的视频服务中,大部分用户观看的视频都是几十秒长的短片。因此,结合视频播放时间使模型能够识别哪些视频是短视频。为此,除了使用 DSNs 之外,我们还建议结合去噪自动编码器SDAE来合并item特征。我们在softmax权重 \(v_k\) 和由去噪自动编码器计算的item的隐藏表示 \(h\) 之间施加均方误差。
整个模型的损失函数如下所示(\(L_{IR}\) 是自动编码器的损失函数):\[E=L_{DSN}+\lambda_{item}L_{item}+\lambda_{IR}L_{IR}\]
\[L_{DSN}=L_{class}+\alpha L_{recon}+\beta L_{difference}+\gamma L_{similarity}\]
\[L_{item}=\mathop{\sum}\limits_{i=1}^{N_s}||v_{yi}-h_i||^2\]
六、参考链接
- https://zhuanlan.zhihu.com/p/49479734