我的推荐算法之路(3):从FM到FFM

发表于 更新于 分类于 阅读次数： 本文字数： 4.5k 阅读时长 ≈ 4 分钟

一、为什么需要特征组合？

在仅利用单一特征而非交叉特征进行判断的情况下，有时不仅是信息损失的问题，甚至会得出错误的结论。著名的“辛普森悖论”用一个非常简单的例子，说明了进行多维度特征交叉的重要性。

辛普森悖论

在对样本集合进行分组研究时，在分组比较中都占优势的一方，在总评中有时反而是失势的一方，这种有悖常理的现象，被称为“辛普森悖论”。

假设表2-1和表2-2所示为某视频应用中男性用户和女性用户点击视频的数据。

表2-1 男性用户
视频 点击（次） 曝光（次） 点击率
视频A 8 530 1.51%
视频B 51 1520 3.36%
表2-2 女性用户
视频 点击（次） 曝光（次） 点击率
视频A 201 2510 8.01%
视频B 92 1010 9.11%

从以上数据中可以看出，无论男性用户还是女性用户，对视频B的点击率都高于视频A，显然推荐系统应该优先考虑向用户推荐视频B。

那么，如果忽略性别这个维度，将数据汇总（如表2-3所示）会得出什么结论呢？

表2-3 数据汇总
视频 点击（次） 总曝光（次） 点击率
视频A 209 3040 6.88%
视频B 143 2530 5.65%

在汇总结果中，视频A的点击率居然比视频B高。如果据此进行推荐，将得出与之前结果完全相反的结论，这就是所谓的“辛普森悖论”。

在辛普森悖论的例子中，分组实验相当于使用“性别”+“视频ID”的组合特征计算点击率，而汇总实验则使用“视频ID”这一单一特征计算点击率。汇总实验对高维特征进行了合并，损失了大量的有效信息，因此无法正确地刻画数据模式。

二、特征交叉的开始——POLY2模型

\[POLY2(w,x)=w_0+\sum_{i=1}^n w_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n w_{ij}x_ix_j\]

可以看到，该模型对所有特征进行了两两交叉（特征 \(x_i\) 和 \(x_j\)），并对所有特征组合赋予权重 \(w_{ij}\) 。\(POLY2\) 通过暴力组合特征的方式，在一定程度上解决了特征组合的问题。但该模型存在两个较大的缺陷：

  • 在处理数据时，经常采用 one-hot 编码的方法处理类别型数据，致使特征向量极度稀疏， \(POLY2\) 进行无选择的特征交叉，使原本就非常稀疏的特征向量更加稀疏，导致大部分交叉特征的权重缺乏有效的数据进行训练，无法收敛。
  • 权重参数的数量由 \(n\) 直接上升到 \(n^2\) ，极大的增加了训练复杂度。

三、因子分解机模型（Factorization Machine, FM）（2010年）

\[ FM(w,x)=w_0+\sum_{i=1}^n w_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n （\vec{v_i}\cdot \vec{v_j}）x_ix_j \]

与 \(POLY2\) 相比，其主要区别是用两个向量的内积 \(（\vec{v_i}\cdot \vec{v_j}）\) 取代了单一的权重系数 \(w_{ij}\) 。具体地说，\(FM\) 为每个特征学习了一个权重隐向量，在特征交叉时，使用两个特征隐向量的内积作为交叉特征的权重。

本质上，\(FM\) 引入隐向量的做法，与矩阵分解用隐向量代表用户和物品的做法异曲同工。可以说， \(FM\) 是将矩阵分解隐向量的思想进行了进一步扩展，从单纯的用户、物品隐向量扩展到了所有特征上。

\(FM\) 通过引入特征隐向量的方式，直接把 \(POLY2\) 模型 \(n^2\) 级别的权重参数数量减少到了 \(nk\) （\(k\) 为隐向量维度， \(n>>k\)），极大地降低了训练开销；而且，隐向量的引入使 \(FM\) 能更好地解决数据稀疏性的问题。比如在 \(POLY2\) 模型中，只有当特征\(x_i,x_j\) 均非零时，才能训练与之对应的 \(w_{ij}\)，而对于 \(FM\) ，每个特征都有其对应的隐向量，减少了训练条件的苛刻性，并且对于未出现的特征组合，只要模型之前分别学习过对应的隐向量，就具备了计算其特征组合权重的能力。

\(FM\) 公式二次项后继推导如下：

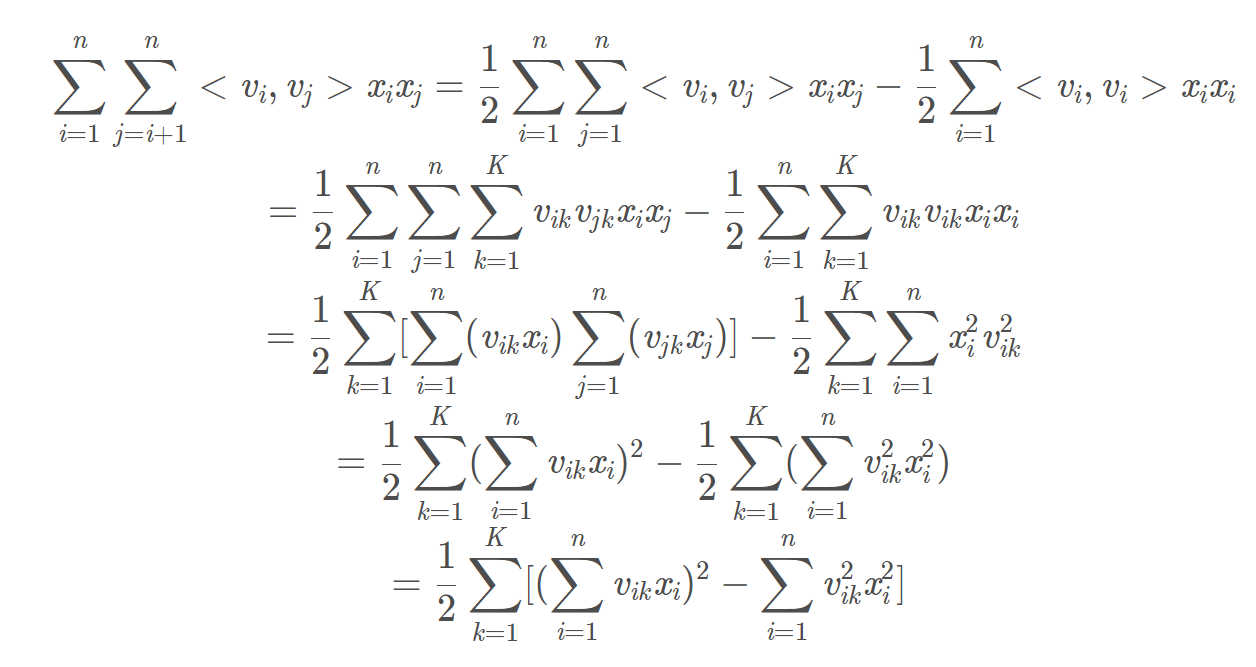
采用梯度下降法求解参数： \[ \frac{∂FM}{∂ \theta}=\begin{cases}1,&\theta=w_0 \cr x_i,&\theta=w_i \cr x_i\sum_{i=1}^n(v_{ik}x_i)-v_{ik}x_i^2,&\theta=v_{ik}\end{cases} \]

四、特征域感知因子分解机模型（Field-aware Factorization Machines，FFM）（2015年）

\[ FFM(w,x)=w_0+\sum_{i=1}^n w_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n （\vec{v_{i，f_j}}\cdot \vec{v_{j,f_i}}）x_ix_j \]

其与 \(FM\) 的区别在于隐向量由原来的 \(\vec{v_i}\) 变成了 \(\vec{v_{i，f_j}}\) ，这意味着每个特征对应的不是唯一一个隐向量，而是一组隐向量。当 \(x_i\) 特征与 \(x_j\) 特征进行交叉时， \(x_i\) 特征会从 \(x_i\) 的这一组隐向量中挑出与特征 \(x_j\) 的域 \(f_j\) 对应的隐向量 \(\vec{v_{i，f_j}}\) 进行交叉。同理， \(x_j\) 也会用与 \(x_i\) 的域 \(f_i\) 对应的隐向量 \(\vec{v_{j，f_i}}\) 进行交叉。

为什么引入Field？

如下表所示，其中性别和年龄同属于user维度特征，而tag属于item维度特征。在FM原理讲解中，“男性”与“篮球”、“男性”与“年龄”所起潜在作用是默认一样的，但实际上不一定。FM算法无法捕捉这个差异，因为它不区分更广泛类别field的概念，而会使用相同参数的点积来计算。

field user field(U) item field(I)
clicked userId Gender_男 Gender_女 Age_[20,30] Age_[30,40] Tag_篮球 Tag_化妆品
1 1 1 0 1 0 1 0
0 1 1 0 1 0 0 1
0 2 0 1 0 1 1 0
1 2 0 1 0 1 0 1

在 \(FFM\)（Field-aware Factorization Machines ）中每一维特征（feature）都归属于一个特定的 \(field\)，\(field\) 和 \(feature\) 是一对多的关系。

\(FFM\) 模型认为 \(v_i\) 不仅跟 \(x_i\) 有关系，还跟与 \(x_i\) 相乘的 \(x_j\) 所属的Field有关系，即 \(v_i\) 成了一个二维向量 \(v_{f×k}\)，\(k\) 是隐向量长度，\(f\) 是Field的总个数。设样本一共有 \(n\) 个特征, 那么 \(FFM\) 的二次项有 \(nf\) 个隐向量。而在 \(FM\) 模型中，每一维特征的隐向量只有一个。\(FM\) 可以看作 \(FFM\) 的特例，是把所有特征都归属到一个 \(field\) 时的 \(FFM\) 模型。

五、FM与FFM的代码实现

5.1 FM

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class FM(nn.Module):
    def __init__(self, n, k):
        super().__init__()
        self.n = n  # 特征个数
        self.k = k  # 隐向量维度
        self.linear = nn.Linear(n, 1, bias=True) # 一次项部分
        self.v = nn.parameter(torch.randn(k, n))  # 隐向量

    def forward(self, x):
        # x: (batch, n)
        part1 = self.linear(x)
        ans1 = torch.pow(torch.mm(x, self.v.t()), 2)
        ans2 = torch.mm(torch.pow(x, 2), torch.pow(self.v.t(), 2))
        return part1 + 0.5 * torch.sum(ans1 - ans2)

5.2 FFM

代码详解参考：推荐系统——FFM模型点击率CTR预估（代码，数据流动详细过程）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import torch
import torch.nn as nn
import numpy as np

class FieldAwareFactorizationMachine(nn.Module):
    def __init__(self, field_dims, embed_dim):
        super().__init__()
        self.num_fields = len(field_dims)
        self.embeddings = torch.nn.ModuleList([
            torch.nn.Embedding(sum(field_dims), embed_dim) for _ in range(self.num_fields)
        ])
        self.offsets = np.array((0, *np.cumsum(field_dims)[:-1]), dtype=np.long)
        for embedding in self.embeddings:
            torch.nn.init.xavier_uniform_(embedding.weight.data)  #初始化

    def forward(self, x):
        x = x + x.new_tensor(self.offsets, dtype=np.long).unsqueeze(0)
        xs = [self.embeddings[i](x) for i in range(self.num_fields)]
        ix = list()
        for i in range(self.num_fields - 1):
            for j in range(i + 1, self.num_fields):
                ix.append(xs[j][:, i] * xs[i][:, j])
        ix = torch.stack(ix, dim=1)

class FieldAwareFactorizationMachineModel(torch.nn.Module):
    def __init__(self, field_dims, embed_dim):
        # field_dims:[10, 20, 30] 共3个field,每个field下各多少特征
        super().__init__()
        self.linear = nn.Linear(sum(field_dims))
        self.ffm = FieldAwareFactorizationMachine(field_dims, embed_dim)

    def forward(self, x):
        """
        :param x: Long tensor of size ``(batch_size, num_fields)``
        """
        ffm_term = torch.sum(torch.sum(self.ffm(x), dim=1), dim=1, keepdim=True)
        x = self.linear(x) + ffm_term
        return torch.sigmoid(x.squeeze(1))