我的推荐算法之路(5):AutoRec
简介
\(AutoRec\) 模型是由澳大利亚国立大学在2015年提出的,它将自编码器(\(AutoEncoder\))的思想与协同过滤(\(Collaborative Filter\))的思想结合起来,提出了一种单隐层的简单神经网络推荐模型。可以说这个模型的提出,拉开了使用深度学习解决推荐系统问题的序幕,为复杂深度学习网络的构建提供了思路。
原文地址:AutoRec: Autoencoders Meet Collaborative Filtering
一、自动编码器AutoEncoder
1.1 自编码器的介绍
自编码器是一种无监督的数据维度压缩和数据特征表达方法,它是神经网络的一种,经过训练后能尝试将输入复制到输出。自编码器由编码器和解码器组成,结构如下:
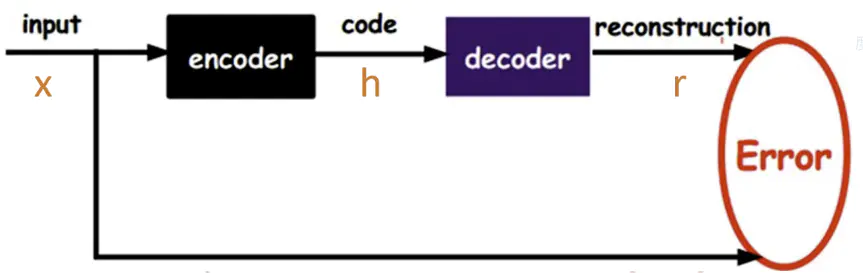
其中,输入为 $x$,输出为 $r$ ,$S$ 代表所有的输入数据向量,$h=f(x)$ 表示编码器,$r=g(h)$ 表示解码器,自编码器的目标便是优化损失函数:\[min \mathop{\sum}\limits_{r \in S} ||r-g(h)||^2_2\]
也就是令图中红色部分的Error值最小。
Q1:输出向量与输入向量误差最小有什么意义?直接使用原始输入向量不行吗?为什么需要编码和解码这些操作?
A1:比如协同过滤中,每个用户对每个物品不可能都评过分,即当数据规模较大时,共现矩阵是一个巨大的稀疏矩阵,该矩阵存在大量的缺失值。故将初始向量通过已训练好的AutoEncoder模型得到的输出向量会因为网络权重的作用而自动填补一些缺失值,与输入向量有所区别。
事实上,AutoEncoder的中间隐层是其最有用的特性之一。其可以作为特征提取的结果,也可作为数据降维的结果等。
Q2:既然共现矩阵稀疏,存在大量缺失值,怎么处理缺失值?训练的效果会好吗?
A2:缺失值的处理可以尝试用0代替,在训练过程中,不同输入向量的不同缺失值相互弥补了输出向量的空缺。个人理解是某些输入向量的训练集中在某些权值上,而另一些与其缺失值不同的输入向量的训练集中在另一些权值上。
1.2 自编码器与前馈神经网络的比较:
- 自编码器是前馈神经网络的一种,最开始主要用于数据的降维以及特征的抽取,随着技术的不断发展,现在也被用于生成模型中,可用来生成图片等。
- 前馈神经网络是有监督学习,其需要大量的标注数据;自编码器是无监督学习,数据不需要标注因此较容易收集。
- 前馈神经网络在训练时主要关注输出层的数据以及错误率;而自编码器可能更多的关注中间隐层的结果。
二、AutoRec
\(AutoRec\) 模型跟多层感知机类似,是一个标准的3层全连接神经网络,只不过它结合了自编码器和协同过滤的思想。再确切一点说,\(AutoRec\) 模型就是一个标准的自编码器结构,它的基本原理是利用协同过滤中的共现矩阵,完成物品向量或者用户向量的自编码,再利用自编码结果得到用户对所有物品的评分,结果通过排序之后就可以用于物品推荐。
2.1 模型结构
在基于评分数据的协同过滤算法中,假设我们有 \(m\) 个用户,\(n\) 个物品,则有用户-物品评分矩阵 \(R \in {\Bbb R}^{m×n}\) 。对于一个用户 \(u\) 来说,他对所有 \(n\) 个物品的评分数据可以形成一个 \(n\) 维的向量 \(r^{(u)}=(R_{u1},\cdots,R_{un})\)。同理,对于一个物品 \(i\) 而言,所有 \(m\) 个用户对它的评分可以构成一个 \(m\) 维的向量 \(r^{(i)}=(R_{1i},\cdots,R_{mi})\) 。其中 \(R_{ui}\) 代表的是用户 \(u\) 对 物品 \(i\) 的评分。
下面是 \(AutoRec\) 的整体模型框图:
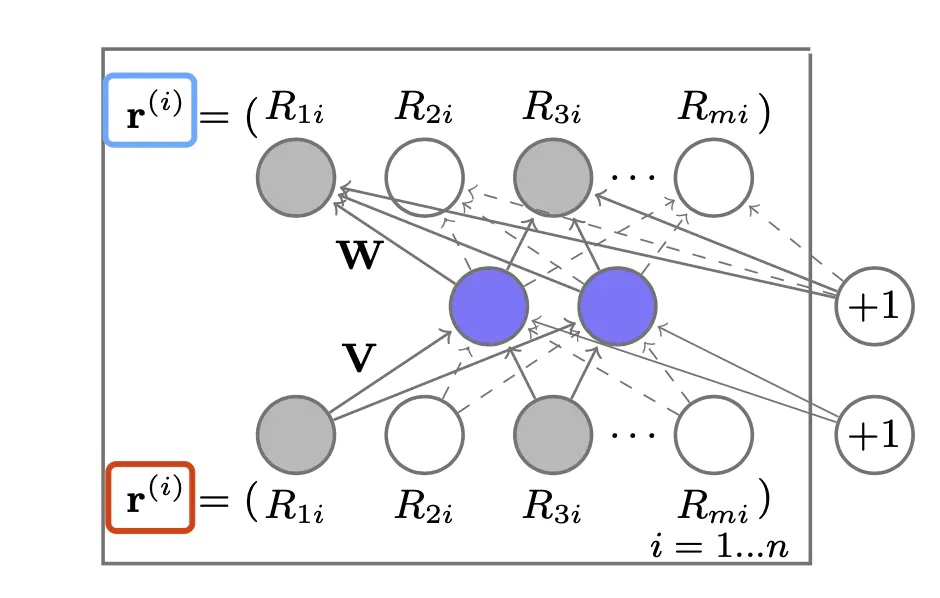
\[h(r;\theta) = f(W·g(Vr+\mu)+b)\]
其中, \(f(·)\) 代表的是输出层的神经元激活函数,\(g(·)\) 代表的是隐层神经元的激活函数。\(\theta=\{W,V,\mu,b\}\),\(V\) 和 \(W\) 分别是隐层和输出层的权重矩阵,\(\mu\) 和 \(b\) 分别是隐层和输出层的偏置。
2.2 损失函数
\[\mathop{min}\limits_{\theta}\sum^n_{i=1}||r^{(i)}-h(r^{(i)};\theta)||^2_2+\frac{\lambda}{2}(||W||^2_2+||V||^2_2)\]
2.3 基于AutoRec的推荐过程
Item-AutoRec
- 依次输入物品 \(i\) 的评分向量 \(r^{(i)}\),得到模型输出的预测评分向量 \(h(r^{(i)};\theta)\);
- 遍历所有物品预测评分向量的第 \(u\) 维,得到用户 \(u\) 对所有物品的评分,进行排序之后得到用户 \(u\) 的推荐列表。
User-AutoRec
- 依次输入用户 \(u\) 的评分向量 \(r^{(u)}\),得到模型输出的预测评分向量 \(h(r^{(u)};\theta)\);
- 进行排序得到用户 \(u\) 的推荐列表。
三、代码演示
1 | import torch |
四、总结
\(AutoRec\) 模型是深度学习方法用于推荐系统中的开山之作,它仅仅使用了一个单隐层的自编码器来泛化用户和物品评分,使模型具有一定的泛化和表达能力。但是由于模型过于简单,也让它在实际使用中显得表征能力不足。