我的推荐算法之路(8):EMCDR
一、跨域推荐概述
为了解决推荐系统冷启动中长期存在的数据稀疏问题,人们提出了跨域推荐(CDR),利用来自更丰富域(源域)的相对更丰富的信息,提高在更稀疏域(目标域)中的推荐性能。
跨域推荐分为两种类型:
- 非对称的方式:利用源域中的数据来解决目标域的数据稀疏性,具体来说是把在源域中学到的知识或者某种模式直接应用到目标域中充当先验或者正则。这种方法的关键之处是需要从源域数据中识别出可以应用到目标域的知识。然而因为没有完全利用源域和目标域的数据,所以是有很大局限的。
- 对称的方式,假设源域和目标域都有数据稀疏的问题,并且它们可以互相应用对方的数据知识。以这种方式来看,这两个域是可以同等对待的,两个域都以协同的方式应对数据稀疏问题。通常这种方式会在域之间学习一个map函数,把域独有的因子和域间共享的因子明确区分开来,主要的缺点是学习域独有的因子和域间共享的因子本身就放大了数据的稀疏性问题。
两种类型的区别在于:非对称方式中源域用于判断label的知识足够多而目标域用于判断label知识相对少,源域需要的知识目标域无法提供,而目标域需要源域的知识,源域知识与目标域知识的交集为目标域知识,这样目标域的知识没必要迁移或迁移过去没多大作用;而对称方式中源域和目标域知识都不太多,有一定交集,也有各自的部分,需要互为补充提高精度。
本篇博客对跨域推荐模型EMCDR做一个详细介绍,原文地址: Cross-Domain Recommendation: An Embedding and Mapping Approach
二、EMCDR模型
2.1 模型总览
EMCDR属于非对称的方式进行跨域推荐,推荐的目标是针对目标域中有很少信息的用户或者物品,例如对于一个新来的用户或者物品,在目标域中并不能找到它的embedding,但是在源域中它比较活跃,可以找到它的embedding,这时通过目标域和源域的map函数(map可以认为是从源域的embedding到目标域embedding的一种映射,所以训练map函数使用的embedding只能是源域和目标域的交叉部分)可以得到目标域的embedding,之后再做推荐。
EMCDR模型如下图所示,其将跨域推荐分为三个步骤:
- Latent Factor Modeling(生成U/I的隐式向量)
- Latent Space Mapping(源域->目标域 U/I隐式向量的映射)
- Cross-domain Recommendation(跨域推荐)
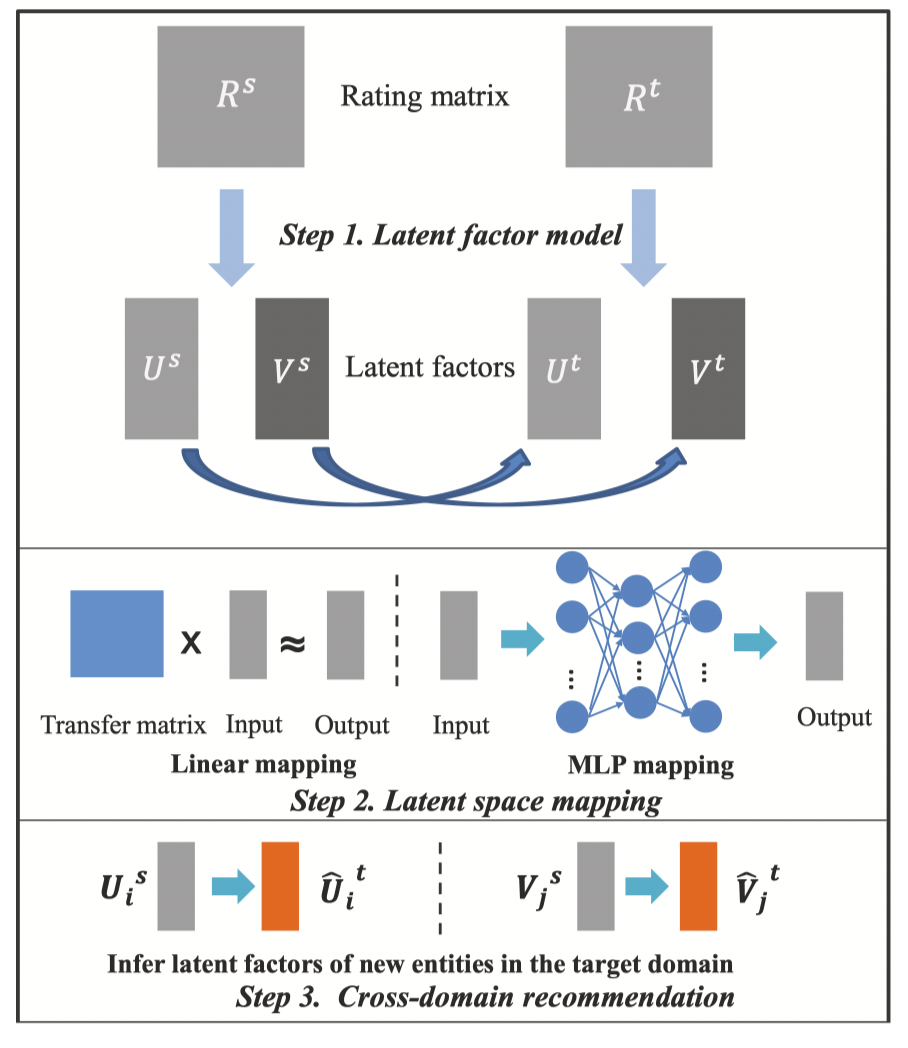
2.2 Latent Factor Modeling
论文中介绍了两种生成隐向量的方式,分别是矩阵分解(MF)和贝叶斯个性化排序(BPR)。
- MF通过构建user-item的二元组,并对其进行矩阵分解生成两个低秩矩阵的乘积。其中,user表示为 \(K \times U\) 的矩阵,item表示为 \(K \times V\) 的矩阵,最终损失函数为:
\[\mathop{min}\limits_{U,V}(\mathop{\sum}\limits_{i}\mathop{\sum}\limits_{j}||I_{ij}\cdot(R_{ij}-U_i^TV_j)||^2_F+\lambda_U\mathop{\sum}\limits_{i}||U_i||^2_F+\lambda_V\mathop{\sum}\limits_{j}||V_j||^2_F)\]
- BPR通过构建user-item1-item2(user对item1的偏好大于item2)的三元组生成user对应的所有商品的全序关系,并通过使用与funkSVD类似的矩阵分解模型生成K维向量,最终的损失函数为:
\[\mathop{min}\limits_{U,V}(\mathop{\sum}\limits_{(u_i,v_j,v_l)\in D}-ln\sigma(U_i^TV_j-U_i^TV_l)+\lambda_U\mathop{\sum}\limits_{i}||U_i||^2_F+\lambda_V\mathop{\sum}\limits_{j}||V_j||^2_F))\]
2.3 Latent Space Mapping
在得到源域和目标域U/I的K维embedding表示后,就可以构建一个map映射关系,完成从源域到目标域的映射。论文中介绍了Linear Mapping、MLP-based Nonlinear Mapping两种映射方法。
- Linear Mapping为线性映射,通过线性变换实现。损失函数表示为:
\[\mathop{min}\limits_{M}\mathop{\sum}\limits_{u_i\in U}L(M\times U_i^s,U_i^t)+\Omega(M)\]
其中,\(U_i^s,U_i^t\) 分别是源域和目标域的隐因子向量,\(M\) 是待学习的线性变换矩阵,\(\Omega(M)\) 是正则项。
- MLP-based Nonlinear Mapping为非线性映射,通过MLP实现。损失函数表示为:
\[\mathop{min}\limits_{\theta}\mathop{\sum}\limits_{u_i\in U}L(f_{mlp}(U_i^s;\theta),U_i^t)\]
其中,\(\theta\) 是MLP的参数。
2.4 Cross-domain Recommendation
对于目标域中信息很少的用户和物品,直接使用MF或者BPR建模出的隐向量是不准确的,有很大偏差。这时可以使用源域建模出的隐向量以及map函数对user建模:
\[\hat{U}_i^t=f(U_i^s;\theta)\]
3、参考链接
- https://zhuanlan.zhihu.com/p/395211316