进击数据挖掘十大算法(八):CART
引言
CART(Classification and Regression Tree),又名分类回归树,是在ID3的基础上进行优化的决策树,CART有以下几个关键点:
- CART既能是分类树,又能是回归树;
- 当CART是分类树时,采用Gini值作为节点分裂的依据;当CART是回归树时,采用样本的最小方差作为节点分裂的依据;
- CART是一棵二叉树。
一、实例
| 看电视时间 | 婚姻情况 | 职业 | 年龄 |
|---|---|---|---|
| 3 | 未婚 | 学生 | 12 |
| 4 | 未婚 | 学生 | 18 |
| 2 | 已婚 | 老师 | 26 |
| 5 | 已婚 | 上班族 | 47 |
| 2.5 | 已婚 | 上班族 | 36 |
| 3.5 | 未婚 | 老师 | 29 |
| 4 | 已婚 | 学生 | 21 |
二、分类树?回归树?
分类树的作用是通过一个对象的特征来预测该对象所属的类别,而回归树的目的是根据一个对象的信息预测该对象的属性,并以数值表示。
CART既能是分类树,又能是决策树,如上表所示,如果我们想预测一个人是否已婚,那么构建的CART将是分类树;如果想预测一个人的年龄,那么构建的将是回归树。
三、CART如何选择分裂的属性?
分裂的目的是为了能够让数据变纯,使决策树输出的结果更接近真实值。那么CART是如何评价节点的纯度呢?如果是分类树,CART采用Gini值衡量节点纯度;如果是回归树,采用样本方差衡量节点纯度。节点越不纯,节点分类或者预测的效果就越差。
Gini值的计算公式:\[Gini=1-\mathop{\sum}\limits_{i \in I}{p_i^2}\]
节点越不纯,Gini值越大。以二分类为例,如果节点的所有数据只有一个类别,则\(Gini=1-\mathop{\sum}\limits_{i \in I}{p_i^2}=0\), 如果两类数量相同,则\(Gini=1-\mathop{\sum}\limits_{i \in I}{p_i^2}=\frac{1}{2}\)。
样本方差计算公式:\[\sigma=\sqrt{\mathop{\sum}\limits_{i \in I}(x_i-\mu)^2}\]
方差越大,表示该节点的数据越分散,预测的效果就越差。如果一个节点的所有数据都相同,那么方差就为0,此时可以很肯定得认为该节点的输出值;如果节点的数据相差很大,那么输出的值有很大的可能与实际值相差较大。
因此,无论是分类树还是回归树,CART都要选择使子节点的GINI值或者回归方差最小的属性作为分裂的方案。即最小化(分类树):\[Gain=\mathop{\sum}\limits_{i \in I}P_i*Gini\]
或者(回归树):\[Gain=\mathop{\sum}\limits_{i \in I}\sigma_i\]
四、CART如何分裂成一棵二叉树?
节点的分裂分为两种情况,连续型的数据和离散型的数据。
CART对连续型属性的处理与C4.5差不多,通过最小化分裂后的 \(Gini\)值 或者 样本方差 寻找最优分割点,将数据一分为二。(对连续值的属性进行排序,\(N\)个数据共\(N-1\)个分裂点,每个分裂点计算\(Gini\)或者样本方差,找使其值最小的分裂点进行二分)
对于离散型属性,理论上有多少个离散值就应该分裂成多少个节点。但CART是一棵二叉树,每一次分裂只会产生两个节点,怎么办呢?很简单,只要将其中一个离散值独立作为一个节点,其他的离散值生成另外一个节点即可。这种分裂方案有多少个离散值就有多少种划分的方法,举一个简单的例子:如果某离散属性一个有三个离散值X,Y,Z,则该属性的分裂方法有{X}、{Y,Z}; {Y}、{X,Z};{Z}、{X,Y},分别计算每种划分方法的 \(Gini\)值 或者 样本方差 确定最优的方法。
划分方法举例:{“学生”}、{“老师”、“上班族”}
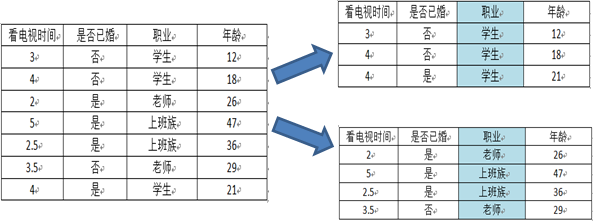
预测是否已婚(分类):
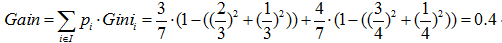
预测年龄(回归):
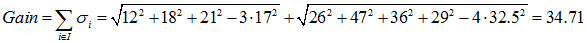
五、停止分裂的条件
(1)最小节点数
当节点的数据量小于一个指定的数量时,不继续分裂。两个原因:一是数据量较少时,再做分裂容易强化噪声数据的作用;二是降低树生长的复杂性。提前结束分裂一定程度上有利于降低过拟合的影响。
(2)熵或者基尼值小于阀值。
由上述可知,熵和基尼值的大小表示数据的复杂程度,当熵或者基尼值过小时,表示数据的纯度比较大,如果熵或者基尼值小于一定程度时,节点停止分裂。
(3)决策树的深度达到指定的条件
节点的深度可以理解为节点与决策树跟节点的距离,如根节点的子节点的深度为1,因为这些节点与跟节点的距离为1,子节点的深度要比父节点的深度大1。决策树的深度是所有叶子节点的最大深度,当深度到达指定的上限大小时,停止分裂。
(4)所有特征已经使用完毕,不能继续进行分裂。
被动式停止分裂的条件,当已经没有可分的属性时,直接将当前节点设置为叶子节点。