我的推荐算法之路(6):Deep Crossing

发表于 2021-10-04 更新于 2022-01-31 分类于推荐算法阅读次数：本文字数： 7.5k 阅读时长 ≈ 7 分钟

一、简介

\(Deep　Crossing\) 模型是微软于2016年在 KDD 上提出的模型，它算是第一个企业以正式论文的形式分享深度学习推荐系统的技术细节的模型。由于手工设计特征（特征工程）花费巨大精力，因此文章提出了\(Deep　Crossing\) 模型自动联合特征与特征交叉。\(Deep　Crossing\) 并没有采用显式交叉特征的方式，而是利用残差网络结构挖掘特征间的关系，以现在的角度看待这个模型是非常简单的，也就是 \(Embedding+MLP\) 的结构，但对当时影响是非常巨大。

原文链接:Deep Crossing: Web-Scale Modeling without Manually Crafted Combinatorial Features

二、模型结构

\(Deep　Crossing\) 一共包含四层结构: \(Embedding\)层、\(Stacking\)层、\(Multiple　Residual　Units\)层、\(Scoring\)层。

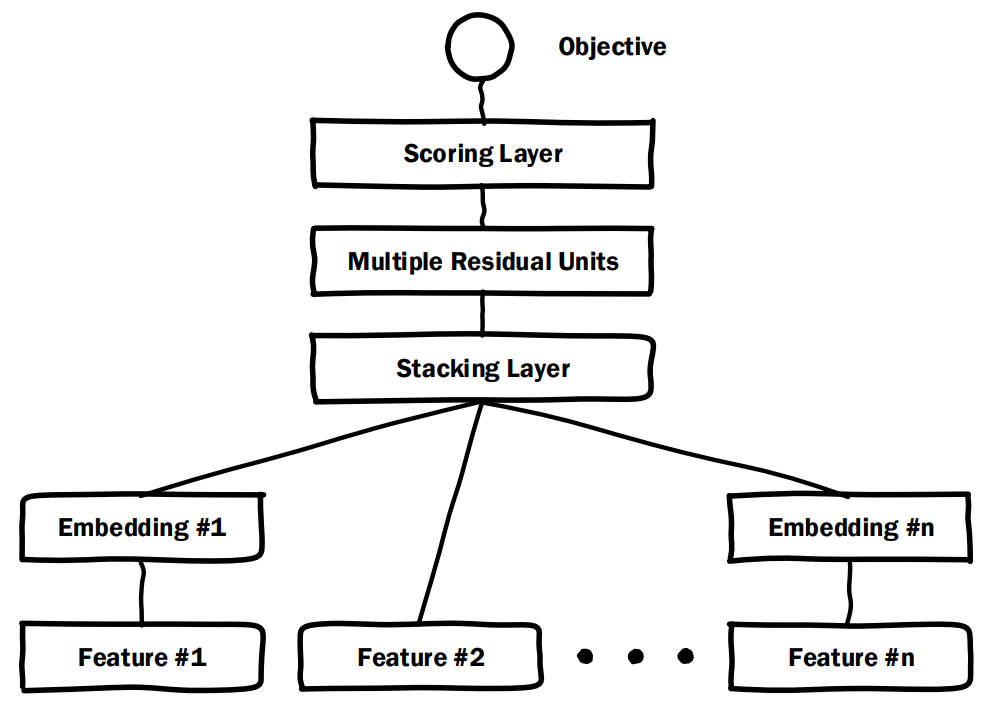
2.1 Embedding Layer

几乎所有基于深度学习的推荐、CTR预估模型都离不开 \(Embedding\) 层，它的作用是将离散高维的稀疏特征转化为低维的密集型特征，其公式化定义为 \(X_j^O=max(0, W_jX_j^I+b_j)\)。其中，\(X_j^I\) 表示经过 \(One-Hot\) 编码的第 \(j\) 个 \(Field\)，\(W_j\) 表示对应的模型参数，\(b_j\) 表示对应的偏置项，\(max\) 操作等价于使用激活函数 \(ReLU\)。在模型结构中发现 Feature #2并没有使用 \(Embedding\)，因为文章提到“维度小于256的特征“不需要进行 \(Embedding\) 转化。

2.2 Stacking Layer

\(Stacking\) 层的操作非常简单，就是将所有的 \(Embedding\) 向量、未进行 \(Embedding\) 操作的原生特征进行拼接，形成一个向量 \(X^O=[X_0^O,X_1^O,\cdots,X_n^O]\)。

2.3 Multiple Residual Units

\(Deep　Crossing\) 模型中的 \(Crossing\) 就是多个残差单元层来实现。该层使用了残差网络的基本单元，单个残差单元如下所示：

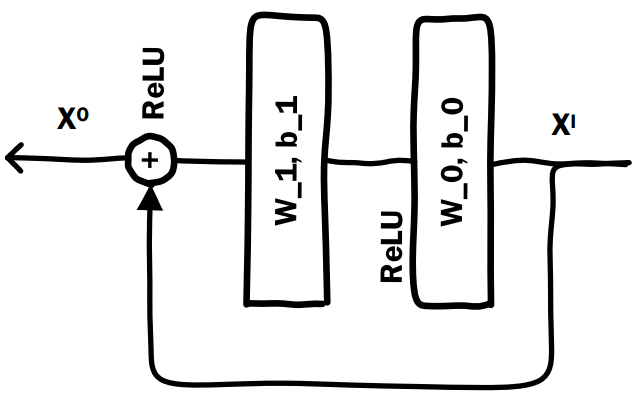
公式定义为：

\[X^O = ReLU(W_1·ReLU(W_0X^I+b_0)+b_1)+X^I\]

\(Deep　Crossing\) 模型使用稍微修改过的残余单元，它不使用卷积内核，改为两层神经网络。可以看到，残差单元是通过两层 \(ReLU\) 变换再将原输入特征加回来。

将 \(X^I\) 移到等式左侧，可以发现左侧变为 \(X^O-X^I\)，可见右侧拟合的是输出与输入之间的残差。有分析说明，残差结构能更敏感的捕获输入输出之间的信息差。

多个残差单元层是 \(MLP\) 的具体实现，该层通过多个残差单元，对特征向量各个维度进行交叉组合，使模型获得了更多的非线性特征和组合特征信息，进而提高了模型的表达能力。

2.4 Scoring Layer

\(Scoring\) 层就是输出层。对于CTR预估模型，往往是一个二分类问题，因此采用逻辑回归来对点击进行预测，损失函数采用交叉熵，激活函数采用 \(Sigmoid\)。

三、伪代码

论文中给出了模型的伪代码，首先定义了一些函数的基本实现：

接着给出了各层的伪代码：

四、代码演示

实验数据选用MovieLens 1M

4.1 数据处理

# 读取users、moives、ratings三个部分的数据
def readMovies(path):
    movies = pd.read_table(os.path.join(path, 'movies.dat'), header=None, sep='::', engine='python')
    movies.columns = ['MovieID', 'Title', 'Genres']
    return movies

def readUsers(path):
    """ Age: {1, 'under 18',  18: "18-24",  25: "25-34",  35: "35-44",
              45: "45-49",    50: "50-55",  56: "56+",}"""
    users = pd.read_table(os.path.join(path, 'users.dat'), header=None, sep='::', engine='python')
    users.columns = ['UserID', 'Gender', 'Age', 'Occupation', 'Zip-code']
    return users

def readRatings(path):
    ratings = pd.read_table(os.path.join(path, 'ratings.dat'), header=None, sep='::', engine='python')
    ratings.columns = ['UserID', 'MovieID', 'Rating', 'Timestamp']
    return ratings

# movielens数据集分为users、movies、ratings三个部分，选择所需的特征将它们合并为一个Tensor
def movieDataConcat(path):  # 合并特征
    ans = []
    users, movies, ratings = readUsers(path), readMovies(path), readRatings(path)
    for row in ratings.values:
        userid, movieid, rating = row[:3]
        gender, age, occupation = users[users.UserID==userid].values[0][1:4]
        genre = movies[movies.MovieID==movieid].Genres.values[0]
        ans.append([userid, gender, age, occupation, movieid, genre, rating])
    np.save('./moviedataconcat.npy', np.array(ans))

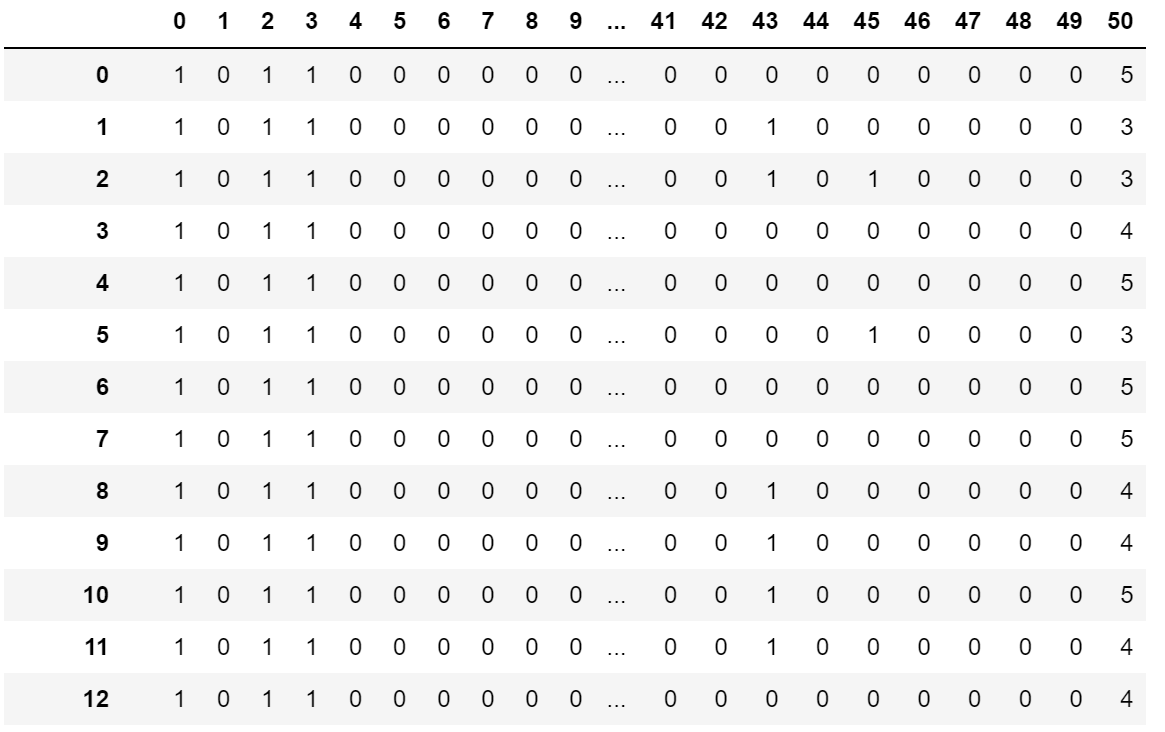
合并结果如下图所示，每个元素的数据类型都是str

4.2 将离散特征转化为One-Hot/Multi-Hot编码

def dataVectorHot(data): 
    # X_type: conVar, 2dim-onehot, 7dim-onehot, 21dim-onehot, conVar, 18dim-multihot, conVar
    strtonum = {'Action' : 0,
                'Adventure' : 1,
                'Animation' : 2,
                'Children\'s' : 3,
                'Comedy' : 4,
                'Crime' : 5,
                'Documentary' : 6,
                'Drama' : 7,
                'Fantasy' : 8,
                'Film-Noir' : 9,
                'Horror' : 10,
                'Musical' : 11,
                'Mystery' : 12,
                'Romance' : 13,
                'Sci-Fi' : 14,
                'Thriller' : 15,
                'War' : 16,
                'Western' : 17}
    ans = []
    for i in range(data.shape[0]):
        tmp = []
        for j in range(data.shape[1]):
            if j == 0 or j == 2 or j == 3 or j == 4 or j == 6:
                tmp.append(int(data[i][j]))
            elif j == 1:
                tmp += ([1, 0] if data[i][j]=='M' else [0, 1])
            else:
                ss = data[i][j].split('|')
                afterchange = [strtonum[s] for s in ss]
                zeros = [0] * 18
                for k in afterchange:
                    zeros[k] = 1
                tmp += zeros
        ans.append(tmp)
    data = np.array(ans)
    change = {1:0,18:1,25:2,35:3,45:4,50:5,56:6} # 为了使用F.one_hot，需要做一个映射
    for i in range(data.shape[0]):
        data[i, 3] = change[data[i, 3]]
    data = torch.tensor(data, dtype=torch.int64)
    data2, data3 = F.one_hot(data[:,3], num_classes=7), F.one_hot(data[:,4], num_classes=21)
    data1, data5 = data[:, 1:3], data[:, 6:24]
    data0, data4, data6 = torch.unsqueeze(data[:,0], dim=1), torch.unsqueeze(data[:,5], dim=1), torch.unsqueeze(data[:,-1], dim=1)
    np.save('./moviedata_vectorform.npy', np.array(torch.cat((data0,data1,data2,data3,data4,data5), dim=1)))

4.3 Residual Unit定义

class ResidualUnit(nn.Module): 
    def __init__(self, innodes, hiddennodes):
        super().__init__()
        self.linear1 = nn.Linear(in_features=innodes, out_features=hiddennodes, bias=True)
        self.linear2 = nn.Linear(in_features=hiddennodes, out_features=innodes, bias=True)
    def forward(self, x):
        return F.relu(self.linear2(F.relu(self.linear1(x))) + x)

4.4 Deep Crossing 模型定义

class DeepCrossing(nn.Module):
    def __init__(self, dense_index, sparse_index, embedding_dim=8, res_hidden=[24, 20, 16, 12, 8]):
        super().__init__()
        self.dense_index = dense_index
        self.sparse_index = sparse_index
        self.embedding_dim = embedding_dim
        self.res_hidden = res_hidden
        self.embedding_layers = nn.ModuleList([
            nn.Embedding(num_embeddings=index[1]-index[0], embedding_dim=self.embedding_dim) for index in self.sparse_index
        ])
        
        self.stack_dim = sum(list(map(lambda x:x[1]-x[0], self.dense_index))) + self.embedding_dim * len(self.sparse_index)
        
        self.residual_layers = nn.ModuleList([
            ResidualUnit(self.stack_dim, h) for h in self.res_hidden
        ])
        
        self.score_layer = nn.Linear(self.stack_dim, 1)
    
    def forward(self, x):
        sparse_embeddings = [self.embedding_layers[idx](x[:, i[0]:i[1]]) \
                             for idx, i in enumerate(self.sparse_index)]
        x = x.float() # x是long类型，embedding的结果是float类型
        sparse_embeddings = [torch.squeeze(torch.matmul(torch.unsqueeze(x[:, i[0]:i[1]],1), sparse_embeddings[idx])) \
                            for idx, i in enumerate(self.sparse_index)]
        sparse_embeddings = torch.cat(sparse_embeddings, -1)

        dense_embeddings = [x[:, i[0]:i[1]] for i in self.dense_index]
        dense_embeddings = torch.cat(dense_embeddings, -1)

        output = torch.cat((dense_embeddings, sparse_embeddings), -1)
        for residual in self.residual_layers:
            output = residual(output)

        result = torch.sigmoid(self.score_layer(output)).squeeze()
        return result

4.5 模型训练

def train(model, lossF, optimizer, train_iter):
    for epoch in range(1000):
        model.train()
        TOTALLOSS, TOTALLEN = 0, 0
        for x, y in train_iter:
            y_pred = model(x)
            l = lossF(y_pred, y.float()).sum()
            TOTALLOSS += l.item()
            TOTALLEN += len(y)
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
        print(TOTALLOSS / TOTALLEN)

if __name__ == '__main__':
    pd.set_option('display.max_rows', 1000, 'display.max_columns',None,
                'display.float_format', lambda x:"%.2f" % x)

    dense_index = [(0, 1), (1, 3), (3, 10), (31, 32)] # 在Tensor中特征对应的起始和结束索引
    sparse_index = [(10, 31), (32, 50)]
    data = torch.tensor(np.load('./moviedata_vectorform.npy'))
    X, Y  = data[:, :-1], data[:, -1]
    train_iter = DataLoader(TensorDataset(X, Y), batch_size=4, shuffle=True)

    dc = DeepCrossing(dense_index, sparse_index)
    optimizer = torch.optim.Adam(dc.parameters(), lr=1e-4, weight_decay=0.1)
    loss = nn.MSELoss()
    train(dc, loss, optimizer, train_iter)

五、其他

在复现论文的时候遇到了一个问题，有关nn.Embedding和nn.Linear的区别，于是结合个人理解稍微记录一下。

其根本区别在于输入，nn.Linear的输入为一个向量，输出也为一个向量，向量的各个维度的元素取值范围是连续的；而nn.Embedding的输入只能为离散值，这个离散值实际上相当于取One-Hot之后的向量。

nn.Embedding() 第一个参数是embedding的数量 \(N\)，第二个参数是embedding后的维度 \(M\)，该函数得到的结果是一个二维矩阵 \(N×M\)。因为embedding的输入是一个One-Hot形式的编码，只有一个维度的值为1，其它均为0。所以，取维度值为1所对应的 \(M\) 维embedding向量和将原始输入(One-Hot向量)与二维矩阵 \(N×M\)做矩阵乘法两者的结果是一样的。原始输入对应着 \(x\)，embedding后得到的二维矩阵为权重矩阵 \(w\)，因此nn.Embedding和nn.Linear的区别就是少了一个偏置项 \(b\)，其它的可以说没什么区别。